Loss Function
개요
손실 함수(Loss function)란?
인공지능은 입력(input)이 들어오면 모델을 통해 예측(predict) 값을 산출합니다.
이 예측 값과 실제 값이 얼마나 유사한지를 판단하는 함수가 loss function입니다.
모델은 이 loss function에서 나오는 loss를 최소화하는 방향으로 가중치(weight)를 조정하므로
loss function은 모델 성능에 큰 영향을 끼칠 수 있습니다.
Loss function 종류
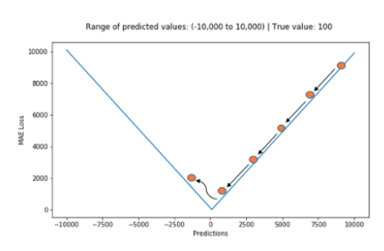
평균 절대 오차(Mean Absolute Error, MAE, L1 Loss)
\[MAE = {1\over N}\sum_{i=1}^n\vert \hat{y_i} - y_i \vert\]특징으로는 전체 데이터의 학습된 정도를 쉽게 파악할 수 있으며
단점으로는 절댓값이기 때문에 예측이 어떤 식으로 발생했는지 판단하기 어렵고
최적 값에 가까워지더라도 이동거리가 일정하기 때문에 최적 값에 수렴하기 어렵습니다.
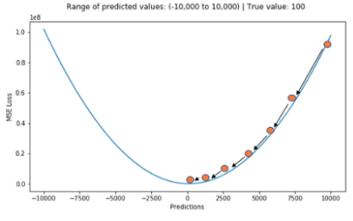
평균 제곱 오차(Mean Square Error, MSE, L2 Loss)
\[MSE = {1\over N}\sum_{i=1}^n ( \hat{y_i} - y_i )^2\]특징으로는 차이가 커질수록 제곱 연산으로 인해 값이 뚜렷해지고
MAE와 달리 최적 값에 가까워질 경우 이동거리가 변화하기 때문에 최적 값에 수렴하기 용이합니다.
단점으로는 MAE < 1일 경우 값은 적어지고 MAE > 1일 경우 값이 커지기 때문에 값의 왜곡이 있을 수 있습니다.
평균 제곱근 오차(Root Mean Square Error, RMSE)
\[RMSE = \sqrt{ {1 \over N} \sum_{i=1}^n ( \hat{y_i} - y_i )^2 }\]MSE와 유사하지만 제곱된 값에 루트를 씌우기 때문에 제곱에서 생기는 왜곡이 줄어듭니다.
그래프는 MAE와 비슷하지만 약간의 굴곡이 있습니다.
Huber Loss
\[l_n = \begin{cases} 0.5 (\hat{y_n} - y_n)^2, & \text{if } |\hat{y_n} - y_n| < delta \\ delta * (|\hat{y_n} - y_n| - 0.5 * delta), & \text{otherwise } \end{cases}\]오차의 절댓값에 따라 계산이 달라지는 Huber loss는
MSE와 MAE를 절충하기 위해 사용됩니다.
Cross-Entropy Loss
Cross Entropy는 Classification 문제에서 loss를 계산할 때 주로 사용합니다.
이것에 대해 설명하기에 앞서 몇가지 개념을 정리하겠습니다.
Entropy
\[H(x) = -\sum_{i=1}^np(x_i)\log p(x_i)\]엔트로피는 불확실성(어떤 데이터가 나올지 예측하기 어려운 것)을 수치적으로 표시해줍니다.
동전과 주사위를 예시로 들면
- 동전을 던졌을 때, 앞/뒷면이 나올 확률 1/2
- 주사위를 던졌을 때, 각 6면이 나올 확률 1/6
이를 계산하면 다음과 같습니다.
\[\begin{align} &H(x_{동전}) = -({1 \over 2}\log{1 \over 2} + {1 \over 2}\log{1 \over 2}) = 0.693 \\&H(x_{주사위}) = -({1 \over 6}\log{1 \over 6} + {1 \over 6}\log{1 \over 6} + {1 \over 6}\log{1 \over 6} + {1 \over 6}\log{1 \over 6} + {1 \over 6}\log{1 \over 6} + {1 \over 6}\log{1 \over 6}) = 1.79 \dots \end{align}\]이렇게 수식적으로 주사위 불확실성을 엔트로피 값으로 표현합니다.
KL-발산(Kullback-Leibler divergence)
\[D_{KL}(p \|| q) = \sum_{i=1}^np(x_i)\log{p(x_i) \over q(x_i)}\]머신러닝은 대부분 정답 분포를 모사하는 모델을 만드는 것이 목표가 됩니다.
그리고 보통 두 분포간의 차이를 이야기할땐 KL-발산이라는 식을 자주 사용합니다.
예시를 들어봅시다.
p(x) = q(x) 라면 항상 이 식의 값은 0이 됩니다.
작을수록 분포가 비슷하다는 것이죠
\(x \in \{a, b\}\)
- 실제 분포 p(a) = 1/3, p(b) = 2/3
- 예측 분포 q(a) = 2/3, q(b) = 1/3
라고 가정하고 KL-발산을 계산하면 \(\begin{align} D_{KL}(p||q) &= \sum_{i=1}^np(x_i)\log{p(x_i) \over q(x_i)} \\& = {1 \over 3}\log{1 \over 2} + {2 \over 3}\log2 \\& = -{1 \over 3}\log2 + {2 \over 3}\log2 \end{align}\)
q(x)가 p(x)보다 클 때는 이점을 주지만, q(x)가 p(x)보다 작은 상황 즉 부족하게 예상을 하면 패널티가 발생합니다.
q(x)나 p(x)나 합은 동일하게 확률값이기에 1 입니다.
따라서 분포가 비슷하게 되려면 “부족하게 예상을 함” 상황을 피해야한다는 것이죠.
\[CE(p, q) = -\sum_{i=1}^np(x_i) \log q(x_i)\]다시 돌아와서
Cross-Entropy 식은 KL-발산 식을 조금 변형하여 얻을 수 있습니다.
\[\begin{align} D_{KL}(p||q) &= \sum_{i=1}^np(x_i)\log{p(x_i) \over q(x_i)} \\& = \sum_{i=1}^np(x_i) \log p(x_i) - \sum_{i=1}^np(x_i) \log q(x_i) \\& = H(p) - \sum_{i=1}^np(x_i) \log q(x_i) \end{align}\]여기서 진분포 $p$를 보면 답이 하나로 정해져 있습니다.
예를 들어 입력 $A$의 분류 클래스가 1이라면 다음과 같습니다
\[\begin{align} &P(X_A = 1) = 1 \\&P(X_A = c) = 0 (c \not= 1) \end{align}\]즉 p의 엔트로피는 0이 되는 겁니다.
KL-발산식을 다시 정리하면
\[D_{KL}(p||q) = -\sum_{i=1}^n p(x_i) \log q(x_i) = CE(p, q)\]Cross-Entropy의 식이 됩니다.
즉 Cross-Entropy를 최소화하는 것은 KL-발산을 최소화하는 것이고
결국 그것은 신경망 모델의 목표인 두 분산의 차이를 줄이는 것입니다.
Binary Cross-Entropy
\[BCE = -{1 \over N} \sum_{i=1}^n y_i \cdot \log (\hat{y_i}) + (1 - y_i) \cdot \log q(1- \hat{y_i})\]0, 1로 구분되는 이진 분류에 사용되는 방식입니다.
Categorical Cross-Entropy
\[CCE = -{1 \over N} \sum_{i=0}^N \sum_{j=0}^C y_j \log(\hat y_j) + (1 - y_j) \cdot \log(1 - \hat y_j)\][0, 0, 1, 0, 0]과 같이 분류해야할 클래스가 3개 이상인 경우(멀티 클래스) 사용됩니다.
NLL loss
\[NLL = -{1 \over N} \sum_{i=0}^N \log (Softmax(x_i))\]단순히 Likelihood의 음로그를 취한 값입니다.
y_i는 softmax 출력 중 가장 큰 값입니다.
입력을 보통 Softmax 함수로 정제한 값을 받기 때문에
log_softmax 함수를 고려하여 pytorch에서는 log를 사용하지 않기도 합니다.
\[Softmax(x_i) = {\exp(x_i) \over \sum_{j} \exp(x_j)}\]softmax 함수를 간단히 살펴보자면
자연 지수함수의 normalization한 함수이기 때문에 합은 무조건 1이 됩니다.
주로 이 함수는 다음처럼 모델 마지막 출력에 대한 확률값을 얻는 데 사용합니다.
<img src=https://blog.kakaocdn.net/dn/kNvMX/btqS3awhvNh/tCSyyqK5CDQWCSUbstdnq0/img.png>
CTC(Connectionist Temporal Classification)
CTC는 time series에 따른 target의 모든 경우의 수 확률의 합입니다.
예를 들면
뉴럴 네트워크는 매 타임 스텝에 문자의 점수를 포함한 행렬을 출력합니다.
다음은 두 번의 타임 스템(t0, t1)과 3개의 경우의 수 문자(‘a’, ‘b’, ‘-‘)들이 존재합니다
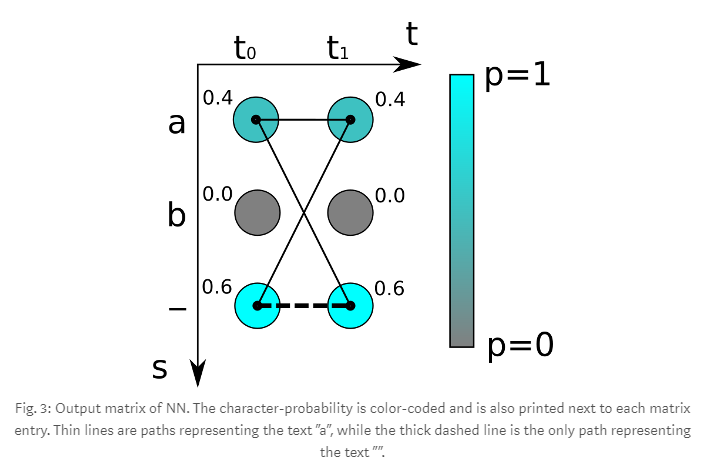
이걸 가지고 ‘aa’ 라는 target의 loss를 구하면
\[loss = -\log(0.4 \times 0.4) = 1.83258...\]이런 식으로 구할 수 있습니다.
Focal Loss
\[FL(p_t) = -(1-p_t)^\gamma \log (p_t)\]Focal loss는 Cross-Entropy loss 함수의 학습 중 클래스 불균형 문제를 해결하기 위해 고안된 함수입니다.
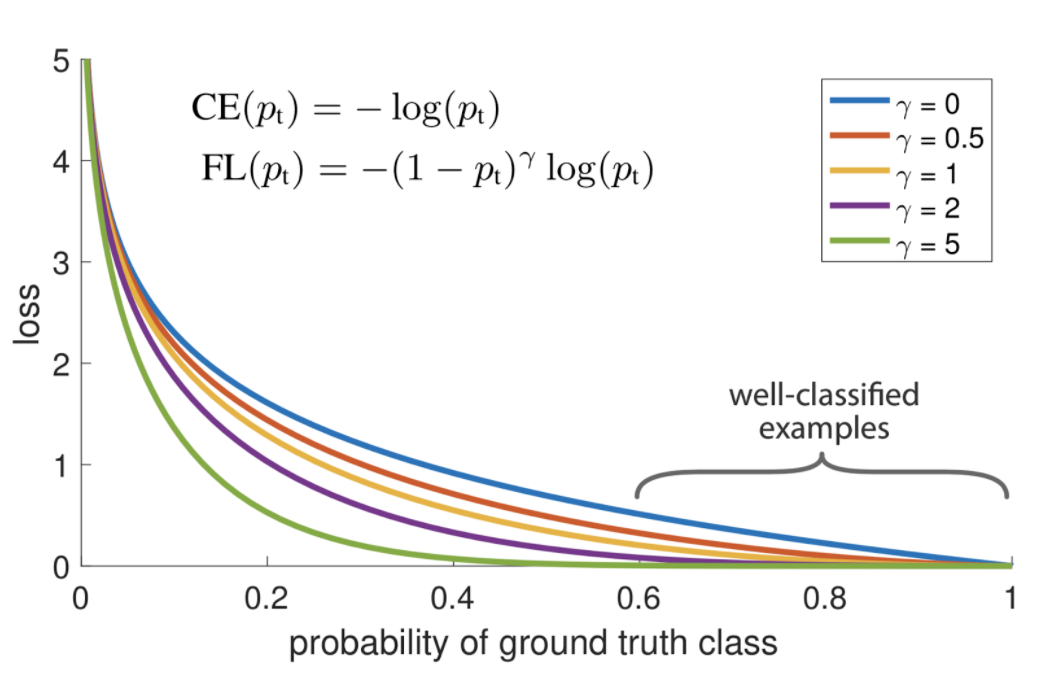
그래프를 보면 알겠지만 focal loss는 $\gamma$ 값에 따라 잘 예측(well-classified)한 데이터에는 Cross-Entropy와 비교하여 패널티를 줍니다.
결국 추가된 $(1-p_t)^\gamma$의 역할은 easy example에 사용되는 loss의 가중치를 줄이기 위함이라고 볼 수 있습니다.
Hinge Loss
스코어 벡터 $s = f(x_i, W)$라고 할 때 Hinge Loss는 다음처럼 표현됩니다.
\[L_i = \sum_{j \neq y_i}^N \max(0, s_i - s_{y_i} + 1)\]SVM(Support Vector Machine)에 주로 사용되는 loss 함수입니다.
SVM
SVM 알고리즘은 기본적으로 두 개의 그룹(데이터)를 분리하는 방법으로
데이터들과 거리가 가장 먼 초평면(hyperplane)을 선택하여 분리하는 방법입니다.
초평면은 두 그룹이 나누어지는 기준 경계라고 할 수 있습니다.
초평면과 데이터 사이에 margin 거리를 margin이라고 하며
최적의 모델은 이 margin을 최대한 줄이는 데에 있습니다.

Triplet Loss
\[L(a, p, n) = \max \{d(a_i, p_i) - d(a_i, n_i) + {\rm margin}, 0\}\]기본적인 아이디어는 동일한 클래스끼리 거리를 더욱 가깝게 만드는 것입니다.
거리 기반 loss 함수로 Anchor(a), Positive(p), Negative(n) 세가지 input을 사용합니다.
- Anchor: 입력 인코딩 벡터
- Positive: 입력과 동일한(positive) 클래스 인코딩 벡터
- Negative: 입력과 다른(negative) 클래스 인코딩 벡터