Pytorch Loss Function
개요
- 개요
- L1Loss
- MSELoss
- CrossEntropyLoss
- CTCLoss
- NLLLoss
- PoissonNLLLoss
- GaussianNLLLoss
- KLDivLoss
- BCELoss
- BCEWithLogitsLoss
- MarginRankingLoss
- HingeEmbeddingLoss
- MultiLabelMarginLoss
- HuberLoss
- SmoothL1Loss
- SoftMarginLoss
- MultiLabelSoftMarginLoss
- CosineEmbeddingLoss
- MultiMarginLoss
- TripletMarginLoss
- TripletMarginWithDistanceLoss
pytorch의 loss function을 정리했습니다.
pytorch 기준이기 때문에 입력으로 넣는 형태에 따라 계산이 달라지기에
계산 방식이 기존 loss function 식과 약간 틀릴 수 있으니 유의하시길 바랍니다.
또한 대부분의 함수들은 reduction이라는 옵션을 통해 loss를 합으로 낼지 합평균으로 낼지 선택할 수 있습니다.
L1Loss
torch.nn.L1Loss(size_average=None, reduce=None, reduction='mean')
L1 베이스(MAE)의 loss function으로
예측 $x$, 목표 $y$ 라고 하면 다음과 같은 식입니다.
\[\ell(x, y) = L = \{ l_1, \dots, 1_N \}^T, \quad l_n \left| x_n - y_n \right|\]MSELoss
torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')
L2 베이스(MSE)의 loss function으로
예측 $x$, 목표 $y$ 라고 하면 다음과 같은 식입니다.
\[\ell(x, y) = L = \{ l_1, \dots, 1_N \}^T, \quad l_n \left( x_n - y_n \right)^2\]CrossEntropyLoss
torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=- 100, reduce=None, reduction='mean', label_smoothing=0.0)
입력으로는 각 클래스에 대해 정규화 되지 않은 점수여야 하며
Tensor의 size는 $(minibatch, C)$ 또는 $(minibatch, C, d_1, d_2, \dots, d_k )$ with $K \geq 1 $ 여야 합니다.
예측 $x$, 목표 $y$, 가중치 $w$, 클래스 갯수 $C$, 미니 배치 $N$ 이라고 하면 다음과 같은 식입니다.
가중치는 각 클래스별 가중치를 주기위한 용도입니다.
ignore 인덱스가 설정되어 있는 경우
\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - w_{y_n} \log \frac{\exp(x_{n,y_n})}{\sum_{c=1}^C \exp(x_{n,c})} \cdot \mathbb{1}\{y_n \not= \text{ignore\_index}\}\]없는 경우
\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - \sum_{c=1}^C w_c \log \frac{\exp(x_{n,c})}{\exp(\sum_{i=1}^C x_{n,i})} y_{n,c}\]식을 살펴보면 식 자체에 소프트맥스 함수가 포함되어 있기에
입력에 따로 소프트맥스 함수 처리를 하지 않아도 됩니다.
CTCLoss
torch.nn.CTCLoss(blank=0, reduction='mean', zero_infinity=False)
CTC는 time series에 따른 target의 모든 경우의 수 확률의 합입니다.
예를 들면
뉴럴 네트워크는 매 타임 스텝에 문자의 점수를 포함한 행렬을 출력합니다.
다음은 두 번의 타임 스템(t0, t1)과 3개의 경우의 수 문자(‘a’, ‘b’, ‘-‘)들이 존재합니다
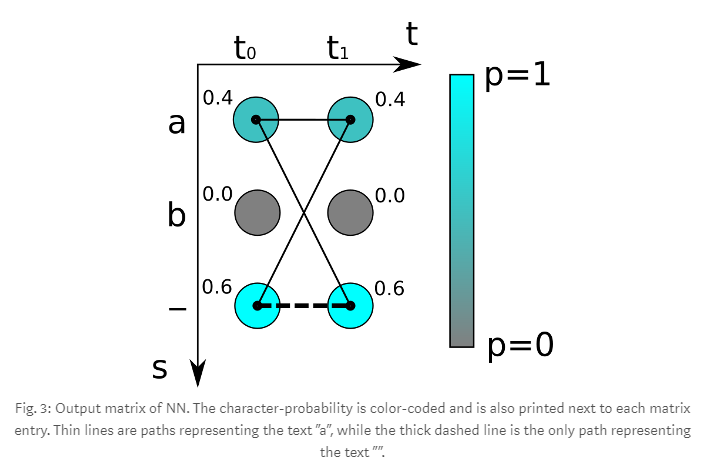
이걸 가지고 ‘aa’ 라는 target의 loss를 구하면
\[loss = -\log(0.4 \times 0.4) = 1.83258...\]이런 식으로 구할 수 있습니다.
pytorch에서는 입력으로 log softmax한 값을 요구합니다.
NLLLoss
torch.nn.NLLLoss(weight=None, size_average=None, ignore_index=- 100, reduce=None, reduction='mean')
NLLLoss(negative log likelihood loss)는 식 자체는 단순합니다.
\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - w_{y_n} x_{n,y_n}, \quad w_{c} = \text{weight}[c] \cdot \mathbb{1}\{c \not= \text{ignore\_index}\}\]LogSoftmax한 값을 입력 받기 때문에 마지막 층에 LogSoftmax 층을 두어야합니다.
그러기 싫다면 이 함수 대신 CrossEntrophyLoss를 대신 사용할 것을 권장합니다.
즉 정리하면 pytorch에서는 NLLLoss + LogSoftmax 층은 CrossEntrophyLoss와 같은 역할을 합니다.
PoissonNLLLoss
torch.nn.PoissonNLLLoss(log_input=True, full=False, size_average=None, eps=1e-08, reduce=None, reduction='mean')
푸아송 분포(Poisson distribution)에 따른 목표 $y$의 NLLLoss 함수입니다.
\[\text{target} \sim \mathrm{Poisson}(\text{input}) \text{loss}(\text{input}, \text{target}) = \text{input} - \text{target} * \log(\text{input}) + \log(\text{target!})\]푸아송 분포에 대해 이야기하기전에 이항 분포에 대해 이야기 합시다.
또 앞서서 조합 기호에 대해 정리하자면 이러합니다.
\[{ {n}\choose{k} } = {_{n}\mathrm{C}_{k}} = { _{n}\mathrm{P}_{k} \over k!} = { n! \over k!(n - k)! }\]이항 분포는 연속된 $n$번의 독립적 시행에서 각 시행이 확률 $p$를 가질 때의 이산 확률 분포입니다.
이러한 시행을 베르누이 시행이라고도 하며 $n=1$일 때 이항 분포는 베르누이 분포라고도 합니다.
확률 변수 $K$가 매개변수 $n$과 $p$를 가지는 이항분포를 따른다면, $K ~ B(n, p)$라고 하며
$n$번 시행 중에 $k$번 성공할 확률은 확률 질량 함수로 다음과 같이 주어집니다.
\[Pr(K = k) = f(k; n, p) = {n \choose k}p^k(1-p)^{n-k}\]예시로 동전을 10회 던져서 앞면 나오는 횟수를 세었다고 가정합시다.
이항 분포 $n=10$이고 앞면이 5번 나왔으므로 $p=1/2$인 이항분포입니다.
그렇다면 동전을 20번 던져서 앞면이 1번 나올 확률은 얼마일까요?
확률 질량 함수로 계산해보면
\[\begin{align} {20 \choose 1}0.5^1(1-0.5)^{20-1} &=20 \times 0.5 \times 0.5^{19} \\&= 1.907348... \times 10^{-5} \\&= 0.001907348 \% \end{align}\]매우 낮은 확률을 확인 할 수 있습니다.
이항 분포는 시행 횟수에 관한 것이라면 푸아송 분포는 단위 시간에 대한 것으로
예시를 들면 동전을 던져 앞면이 나올 확률을 모른다고 가정 했을 때
동전을 초당 한번 10초 동안 던져서 앞면이 5번 나올 때 20초 던져서 앞면이 나오지 않을 확률에 대한 분포입니다.
10초에 5번 20초면 10번은 앞면이 평균적으로 나옵니다.
시간 간격을 매우 짧게 즉 시행 횟수 $n$을 무한으로 보면
$p$는 0으로 수렴하게 되고 이항 분포의 평균인 $np$를 $\lambda$로 놓고 보면
\[\begin{aligned} \lim_{n \to \infty} B(k; n, p) = & \lim_{n \to \infty} { {n}\choose{k} } p^k(1-p)^{n-k} \\ = & \lim_{n \to \infty} \dfrac{n!}{k!(n-k)!}(\dfrac{\lambda}{n})^k (1-\dfrac{\lambda}{n})^{n-k} \\ = & \lim_{n \to \infty} \underset{(가)}{\left[ \dfrac{n!}{(n-k)! n^k} \right]} \left[ \dfrac{\lambda^k}{k!} (1-\dfrac{\lambda}{n})^{n} \right] \underset{(나)}{\left[ (1-\dfrac{\lambda}{n})^{-k}\right]} \\ = & 1\left[ \dfrac{\lambda^k}{k!} e^{-\lambda}\right] 1 \\ = & f(k; \lambda) \\ & \text{(푸아송 분포의 확률 질량 함수)} \end{aligned}\]GaussianNLLLoss
KLDivLoss
torch.nn.KLDivLoss(size_average=None, reduce=None, reduction='mean', log_target=False)
쿨백-라이블리 발산 베이스의 loss 함수로
NLL loss처럼 로그 확률을 입력으로 받습니다.
\[l(x,y) = L = \{ l_1,\dots,l_N \}, \quad l_n = y_n \cdot \left( \log y_n - x_n \right)\]BCELoss
torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction='mean')
Binary Cross Entropy 베이스의 loss 함수입니다.
binary이기 때문에 $x$와 $y$ 값의 범위는 [0, 1]로 제한됩니다.
\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - w_n \left[ y_n \cdot \log x_n + (1 - y_n) \cdot \log (1 - x_n) \right]\]$y_n = 0$ 이거나 $(1-y_n) = 0$ 일 경우 결과 값이 $-\infin$가 될 수 있는데
이럴 경우 -100으로 clamp를 합니다.
BCEWithLogitsLoss
torch.nn.BCEWithLogitsLoss(weight=None, size_average=None, reduce=None, reduction='mean', pos_weight=None)
Sigmoid 층을 합한 BCELoss이지만
수학적으로 일반적인 Sigmoid 층보다 log-sum-exp에서 더 안정적이라고 합니다.
\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - w_n \left[ y_n \cdot \log \sigma(x_n) + (1 - y_n) \cdot \log (1 - \sigma(x_n)) \right]\]MarginRankingLoss
torch.nn.MarginRankingLoss(margin=0.0, size_average=None, reduce=None, reduction='mean')
유사도 학습(Metric Learning)을 위한 loss인 듯 하다.
HingeEmbeddingLoss
torch.nn.HingeEmbeddingLoss(margin=1.0, size_average=None, reduce=None, reduction='mean')
hinge는 경첩이라고 하며 주로 SVM에 사용됩니다.
\[l_n = \begin{cases} x_n, & \text{if}\; y_n = 1,\\ \max \{0, \Delta - x_n\}, & \text{if}\; y_n = -1, \end{cases}\]MultiLabelMarginLoss
torch.nn.MultiLabelMarginLoss(size_average=None, reduce=None, reduction='mean')
HuberLoss
torch.nn.HuberLoss(reduction='mean', delta=1.0)
MSE 보다 데이터의 이상 값에 덜 민감하며 기본적으로 MAE이며
오차가 작으면 MSE로 계산하는 방식입니다.
SmoothL1Loss
torch.nn.SmoothL1Loss(size_average=None, reduce=None, reduction='mean', beta=1.0)
SoftMarginLoss
torch.nn.SoftMarginLoss(size_average=None, reduce=None, reduction='mean')
MultiLabelSoftMarginLoss
torch.nn.MultiLabelSoftMarginLoss(weight=None, size_average=None, reduce=None, reduction='mean')
CosineEmbeddingLoss
torch.nn.CosineEmbeddingLoss(margin=0.0, size_average=None, reduce=None, reduction='mean')
MultiMarginLoss
torch.nn.MultiMarginLoss(p=1, margin=1.0, weight=None, size_average=None, reduce=None, reduction='mean')
TripletMarginLoss
torch.nn.TripletMarginLoss(margin=1.0, p=2.0, eps=1e-06, swap=False, size_average=None, reduce=None, reduction='mean')
TripletMarginWithDistanceLoss
torch.nn.TripletMarginWithDistanceLoss(*, distance_function=None, margin=1.0, swap=False, reduction='mean')